Сколько комбинаций в покере

Вопрос «Какие карты у оппонента?» интересен новичкам и профессиональным игрокам за столом. От ответа зависят характер и содержание раздачи, шансы на победу. Количество комбинаций известно (их десять). Но нужно знать и варианты их составления, чтобы сделать оценку диапазона оппонента. В статье — о способах расчета возможных рук соперника, применении знаний о комбинациях в покере.
Содержание
Что такое комбинаторика в покере
Игроки во время раздачи считают ауты — карты, позволяющие составить сильную руку. Они имеют большое значение, поскольку оказывают влияние на принятие решений. Комбинаторика — математический метод расчета количества комбинаций с конкретными вариантами рук в определенных ситуациях. Благодаря анализу с применением формул открывается важная информация:
- Количество вариантов сочетания 7-7.
- Способы сдачи A-K или других сильных рук.
- Количество стрит-дро, которые могут быть при флопе A-10-7.
Новички не используют математику из-за мнения, что расчеты сложны. Но это доступные знания и сила покериста. Достаточно перемножить цифры, и стратегия станет более выигрышной.
Для чего нужны знания комбинаторики
Инструмент позволяет:
- Дать оценку раздачи и своего участия в ней.
- Предположить количественный диапазон возможных стартовых рук оппонента.
- Повысить качество блефа.
- Находить оптимальные, выигрышные решения.
Профессиональные покеристы применяют методы подсчета в каждой раздаче. Цифры и математика превращаются в шансы, сложные ситуации — в простые. Вычисление вероятного количества вариаций рук соперника повышает умение анализировать. Это важное условие развития уровня игры.
Например, покерист на префлопе делает рейз с 10-10. Очень тайтовый соперник отвечает ходом в олл-ин. В такой ситуации игроки идут ва-банк с сильной карманной парой (J-J, Q-Q, K-K), бигсликом (A-K) или префлоп-натсом (A-A). По подсчетам возможны 24 карманных комбо (6 х 4) + 16 одно- и разномастных вариантов A-K. Итого: 16 / 40 = с вероятностью в 40% покерист играет против A-K, в 60% (24 / 40) соперник покажет оверпару. Комбинаторика открыла простую истину: коинфлип не выгоден по шансам.
Расчеты в уме частично заменяет покерный софт. Но в большинстве румов он запрещен, а в живой игре программу открывать нельзя.
Комбинаторика на префлопе
На первом этапе торговли анализ вероятных карманок противника даст ценную информацию. Общий смысл на примере Техасского Холдема: на руках у оппонента могут быть пары, разно- или одномастные варианты. Метод подсчета дает сделать количественную оценку.
| Модель или вероятность | Количество |
| Возможные руки в непарных вариантах с одинаковым номиналом | 16 |
| Парные сочетания | По 6 (одного достоинства) |
| Все варианты комбинаций на префлопе | 1,326 (общее число) |
| Способы комбинирования разномастных рук | 12 |
Для непарных рук
Вероятность получения игроком одномастных рук разного номинала меньше, чем аналогичных разномастных сочетаний. Существует 16 вариантов из любых 2 случайных непарных карт. Из них 4 — комбинации одной масти и 12 — разной. Всего непарные руки составляют 94% от общего количества (1,248 вариантов).
Для парных рук
В Техасском Холдеме из 1,326 вариаций стартовых рук только 6% будут одинаковыми по номиналу. В абсолютном выражении — 78 комбо. Расчет за столом простой: каждая пара может быть в 6 разных вариациях. При анализе ситуации цифра умножается на количество возможных рук в диапазоне.
Количество комбинаций в покере
Традиционно игроки за столом собирают сочетания из 7 карт. Количество комбинаций в покере — 10:
- Старшая карта
- Пара
- Две пары
- Сет (тройка, трипс)
- Стрит
- Флеш
- Фулл-хаус
- Каре
- Стрит-флеш
- Роял-флеш.

Классические покерные комбинации
В контексте комбинаторики в покере сочетания изучаются как основы для составления рук. В Техасском Холдеме возможны 133,784,560 различных семикарточных (карманки + борд) вариаций. Сила готового сочетания прямо зависит от вероятности его сбора.
Например, подсчет шансов получения каре по системе комбинаторного анализа. Всего вариаций сочетания 13 (4 двойки, тройки, четверки и т. д.). Из колоды в 52 карты вычитаются 4 (они составляют каре). Получается 48. Цифра нужна для расчета по 3 оставшимся в готовой комбинации картам. В общем они могут составить 17,296 сочетаний. 17,296 х 13 = 224,848 способов получения каре. Вероятность сбора комбинации = 224,848 / 133,784,560 х 100 = 0.168%.
Комбинаторика на постфлопе
Для определения количественной вероятности рук в диапазоне оппонента после появления борда используются две модели. Один расчет — для парных сочетаний, другой — для непарных. Применяемая формула:
O (искомое число) = K1 x K2 или K x (K−1) / 2.
Для непарных рук
У игрока A-Q. На борде A-J-5. Расчет возможного числа комбо вида A-K у соперников:
- K1 — доступные карты, равные по номиналу первой карманной карте (тузы).
- K2 — свободные варианты с рангом второй искомой переменной (короли).
K1 = 4 (всего тузов в колоде) − 2 (у игрока и на борде) = 2. K2 = 4 (в руке и на доске королей нет). K1 * K2 = 2 x 4 = 8 потенциальных вариантов сбора A-K противником.
Для парных рук
Анализ на основе данных из прошлого примера. Формула для парных карманок меняется:
- K — все свободные карты номинала первой искомой (туза).
- K − 1 — полученное число K минус 1 единица.
K = 4 (по количеству тузов в колоде) − 2 (у игрока и на борде) = 2. K1 = 2 − 1 = 1. K * (K-1) / 2 = 2 x 1 / 2 = 1 возможный вариант сбора A-K. Больше одного оппонента с такой рукой за столом быть не может.
Вычисление способов сбора комбинации критически важно для анализа ситуации.
Логически и математически тайтовый оппонент с узким диапазоном играет с A-A, A-K, K-K с вероятностью в 33%. Но модель комбинаторики подсказывает: из-за разницы в количественных шансах сбора парных сочетаний цифры совсем другие. A-K — 57%, A-A и K-K — по 21.5%.
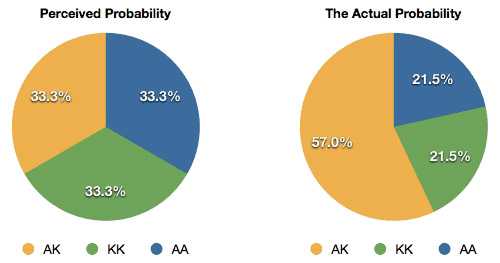
Наглядный пример работы комбинаторного метода
Эффект изъятия карт или блокеры
В расчетах и формулах есть центральная переменная. Свободные карты влияют на итоговое число. Если у игрока или на борде есть условный туз, его не будет в диапазоне рук оппонента. Количество возможных комбинаций снижается. Такой туз называют блокером и исключают при расчете.
Пример. У игрока K-K. Доска 10-9-2. Возможных вариантов сетов 9 (по 3 пары десяток, девяток и двоек). Меняем K-K на A-10. Десятка блокирует карманные пары. Теперь число составления сетов не 9, а 7 (1 + 3 + 3).
Использование комбинаторики в различных ситуациях
Математика не выигрывает раздачи. Шансы не означают гарантию победы. Методы комбинаторики профессионалы сочетают с ридсами, собственной тактикой и стратегией. Наблюдение за соперником помогает определить его стиль и понять диапазон. Расчеты позволяют сузить процент возможных вариантов и конвертировать все в инструмент для успешной игры. Комбинации в покере собираются по воле случая, но зависят от законов математики.
Например, покерист с рукой 7-7, на борде A-Q-7-8-2. Банк — $12. После ставки в $10 оппонент отвечает пушем в $60. По шансам банка колл возможен, если покерист в 38% случаев впереди соперника. Комбинаторика позволяет рассмотреть все возможные руки противника и вероятности их составления. Итоги:
- Всего возможных вариантов комбо — 42.
- Сочетаний, которые проиграют сету семерок — 33.
- Победных в сравнении с 7-7-7 вариантов — 9.
79% (по эквити) на 21% в пользу игрока. Колл оправдан.
Часто задаваемые вопросы
Пользоваться статистикой с помощью ридсов и анализа во время игры.
Большинство профессионалов используют все инструменты математики. Одну раздачу или турнир можно выиграть на везении, серию — нет.
Покерист начинает играть не по своим, а по чужим рукам. Такого противника очень трудно прочитать.
Всегда изучать свои руки в программах. Со временем типовые ситуации будут запоминаться автоматически, расчет станет легче.
На столах формата NL5 много рекреационных игроков. Они не думают, предугадать их ходы и диапазоны сложнее.



